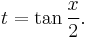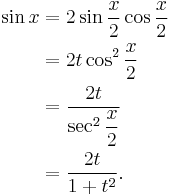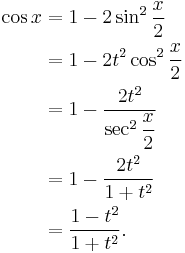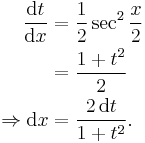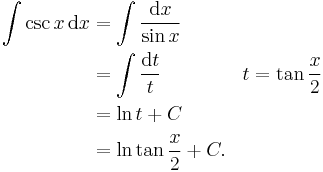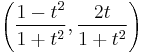Weierstrass substitution

In integral calculus, the Weierstrass substitution, named after Karl Weierstrass, is used for finding antiderivatives, and hence definite integrals, of rational functions of trigonometric functions. No generality is lost by taking these to be rational functions of the sine and cosine. The substitution involves tangents of half-angles. Michael Spivak wrote that "The world's sneakiest substitution is undoubtedly" this technique.[1]

Contents

The substitution

One starts with the problem of finding an antiderivative of a rational function of the sine and cosine, and replaces sin x, cos x, and the differential dx with rational functions of a variable t and the product of a rational function of t with the differential dt, as follows:[2]

\begin{align} \sin x & = \frac{2t}{1 %2B t^2} \\[8 pt] \cos x & = \frac{1 - t^2}{1 %2B t^2} \\[8 pt] \mathrm{d}x & = \frac{2 \,\mathrm{d}t}{1 %2B t^2}. \end{align}

Derivation

Let

t = \tan\frac{x}{2}.

By the double-angle formula for the sine function,

\begin{align} \sin x&=2\sin\frac{x}{2}\cos\frac{x}{2}\\ &=2t\cos^2\frac{x}{2}\\ &=\frac{2t}{\sec^2\dfrac{x}{2}}\\ &=\frac{2t}{1%2Bt^2}. \end{align}

By the double-angle formula for the cosine function,

\begin{align} \cos x&=1-2\sin^2\frac{x}{2}\\ &=1-2t^2\cos^2\frac{x}{2}\\ &=1-\frac{2t^2}{\sec^2\dfrac{x}{2}}\\ &=1-\frac{2t^2}{1%2Bt^2}\\ &=\frac{1-t^2}{1%2Bt^2}. \end{align}

The differential dx can be calculated as follows:

\begin{align} \frac{\mathrm{d}t}{\mathrm{d}x}&=\frac{1}{2}\sec^2\frac{x}{2}\\ &=\frac{1%2Bt^2}{2}\\ \Rightarrow\mathrm{d}x&=\frac{2\,\mathrm{d}t}{1%2Bt^2}. \end{align}

Examples

First example

(See also integral of the secant function.)

\begin{align} \int\csc x\,\mathrm{d}x&=\int\frac{\mathrm{d}x}{\sin x}&\\ &=\int\frac{\mathrm{d}t}{t}&t=\tan\frac{x}{2}\\ &=\ln t%2BC\\ &=\ln \tan\frac{x}{2}%2BC. \end{align}

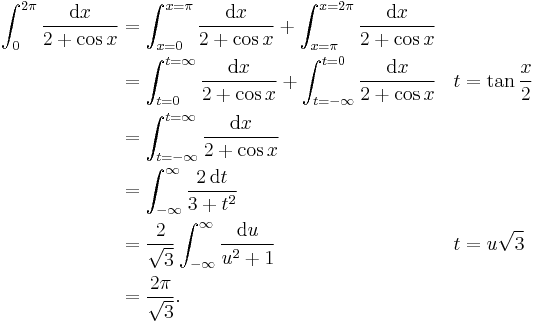
Second example: a definite integral

\begin{align} \int_0^{2\pi}\frac{\mathrm{d}x}{2%2B\cos x}&=\int_{x=0}^{x=\pi}\frac{\mathrm{d}x}{2%2B\cos x}%2B\int_{x=\pi}^{x=2\pi}\frac{\mathrm{d}x}{2%2B\cos x}&&\\ &=\int_{t=0}^{t=\infty}\frac{\mathrm{d}x}{2%2B\cos x}%2B\int_{t=-\infty}^{t=0}\frac{\mathrm{d}x}{2%2B\cos x}&t&=\tan\frac{x}{2}\\ &=\int_{t=-\infty}^{t=\infty}\frac{\mathrm{d}x}{2%2B\cos x}&&\\ &=\int_{-\infty}^{\infty}\frac{2\,\mathrm{d}t}{3%2Bt^2}&&\\ &=\frac{2}{\sqrt 3}\int_{-\infty}^{\infty}\frac{\mathrm{d}u}{u^2%2B1}&t&=u\sqrt 3\\ &=\frac{2\pi}{\sqrt 3}.&& \end{align}

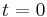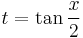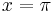In the first line, one cannot simply substitute t=0 for both limits of integration. The singularity (in this case, a vertical asymptote) of t=\tan\frac{x}{2} at x=\pi must be taken into account.

Geometry

As x varies, the point (cos x, sin x) winds repeatedly around the unit circle centered at (0, 0). The point

\left(\frac{1-t^2}{1%2Bt^2}, \frac{2t}{1%2Bt^2}\right)

goes only once around the circle as t goes from −∞ to +∞, and never reaches the point (−1, 0), which is approached as a limit as t approaches ±∞. As t goes from −∞ to −1, the point determined by t goes through the part of the circle in the third quadrant, from (−1, 0) to (0, −1). As t goes from −1 to 0, the point follows the part of the circle in the fourth quadrant from (0, −1) to (1, 0). As t goes from 0 to 1, the point follows the part of the circle in the first quadrant from (1, 0) to (0, 1). Finally, as t goes from 1 to +∞, the point follows the part of the circle in the second quadrant from (0, 1) to (−1, 0).

Here is another geometric point of view. Draw the unit circle, and let P be the point (−1, 0). A line through P (except the vertical line) is determined by its slope. Furthermore, each of the lines (except the vertical line) intersects the unit circle in exactly two points, one of which is P. This determines a function from points on the unit circle to slopes. The trigonometric functions determine a function from angles to points on the unit circle, and by combining these two functions we have a function from angles to slopes.

See also

Notes and references

  1. ^ Michael Spivak, Calculus, Cambridge University Press, 2006, pages 382–383.
  2. ^ James Stewart, Calculus: Early Transcendentals, Brooks/Cole, 1991, page 439

External links